How to Find the Volume and Surface Area of a Triangular Prism?

The prism is a solid shape with flat faces, two identical bases, and the same cross-section along its entire length. The name of a particular prism depends on the two bases of the prism, which can be triangular, rectangular, or polygonal.

Related Topics

• How to Find the Volume and Surface Area of Rectangular Prisms?

A step-by-step guide to finding the volume and surface area of triangular prism

A triangular prism is a three-dimensional polyhedron with three rectangular faces and two triangular faces. The \(2\) triangular faces are congruent to each other, and the \(3\) lateral faces which are in the shape of rectangles are also congruent to each other. Thus, a triangular prism has \(5\) faces, \(9\) edges, and \(6\) vertices.

See the image below of a triangular prism where \(l\) represents the length of the prism, \(h\) represents the height of the base triangle, and \(b\) represents the bottom edge of the base triangle.

Triangular prism properties

The properties of a triangular prism help us to easily identify it. The following are some features of a triangular prism:

• A triangular prism has \(5\) faces, \(9\) edges, and \(6\) vertices.
• It is a polyhedron with \(3\) rectangular faces and \(2\) triangular faces.
• The two triangular bases are congruent with each other.
• Any cross-section of a triangular prism is in the shape of a triangle.

Triangular prism formulas

There are two important formulas for a triangular prism, which are surface area and volume.

The volume of a triangular prism

The volume of a triangular prism is the product of its triangular base area and the length of the prism. As we already know that the base of a triangular prism is in the shape of a triangle. So,

\(\color{blue}{Volume\:of\:a\:triangular\:prism\:=\:area\:of\:base\:triangle\:×\:length\:=\frac{1}{2}\:×\:b\:×\:h\:×\:l}\)

where,

• \(b\) is the base length of the triangle,
• \(h\) is the height of the triangle,
• \(l\) is the length of the prism.

The surface area of a triangular prism

The surface area of a triangular prism is the area occupied by the surface. It is the sum of the areas of all the faces of the prism. Therefore, the formula to calculate the surface area is:

\(\color{blue}{Surface\:area\:=\left(Perimeter\:of\:the\:base\:×\:Length\:of\:the\:prism\right)\:+\:\left(2\:×\:Base\:Area\right)\:=\:\left(S_1\:+S_2\:+\:S_3\right)L\:+\:bh}\)

where,

• \(b\) is the lower edge of the base triangle,
• \(h\) is the height of the base triangle,
• \(L\) is the length of the prism,
• \(S_1, S_2,\) and \(S_3\) are the three edges (sides) of the base triangle,
• \((bh)\) is the combined area of the two triangular faces because \(\left[2\:×\:\left(\frac{1}{2}\:×\:bh\right)\right]\:=\:bh\).

The lateral surface area of the triangular prism

The lateral surface area of any solid is the area without the bases. In other words, the lateral surface area of a triangular prism is calculated without considering the base area. Thus, the lateral surface area of a triangular prism is:

\(\color{blue}{Lateral\:surface\:area =\:\left(S_1\:+\:S_2\:+\:S_3\right)\:×\:l\:=\:\left(Perimeter\:×\:Length\right)\:or\:LSA=\:p\:×\:l}\)

where,

• \(l\) is the height (length) of a prism
• \(p\) is the perimeter of the base

Finding the Volume and Surface Area of Triangular Prism – Example 1:

Find the volume of a triangular prism where the base of the triangle is \(8\:??\:\), its height is \(6\:??\:\), and the length of the prism is \(10\:??\:\).

Solution:

The base of the triangle is \((b) = 8\space in\), and the height of the triangular base \((h) = 6\space in\).

So, the base area \(= (\frac{1}{2})(bh) = (\frac{1}{2}) × (8 × 6) = \frac{48}{2}=24\space in^2\).

The length of the prism is \(L = 10\space in\).

Using the volume of the triangular prism formula,

The volume of the given triangular prism \(=base\:area\:×\:length\:of\:the\:prism = 24 × (10) = 240\space in^3\).

Exercises for Finding the Volume and Surface Area of Triangular Prism

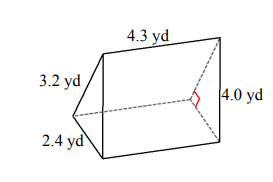
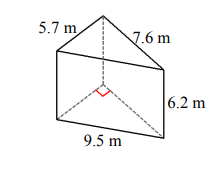
Find the volume and surface area for each triangular prism.

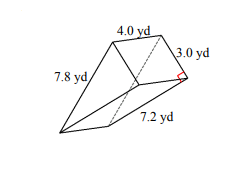
1. \(\color{blue}{V=43.2\:yd^3, A=93.6\:yd^2}\)
2. \(\color{blue}{V=16.5\:yd^3, A=49\:yd^2}\)
3. \(\color{blue}{V=134.3\:m^3, A=184.7\:m^2}\)