The Unit Circle

The location of a point that is a distance of one unit from a fixed point is called a unit circle.

Related Topics

• How to Solve Angles and Angle Measure

A step-by-step guide to the unit circle

A unit circle is a circle with a radius of \(1\) unit. The unit circle is generally shown on the Cartesian coordinate plane. The unit circle is represented algebraically using the second-degree equation with two variables \(x\) and \(y\). The unit circle is used in trigonometry and is useful for finding the values of the trigonometric ratios of sine, cosine, and tangent.

Equation of a unit circle

The general equation of a circle is \((x-a)^2+(y-b)^2=r^2\), which represents a circle having the center \((a, b)\) and the radius \(r\). This equation of a circle is simplified to show the equation of a circle. A unit circle is formed with its center at the point\((0, 0)\), which is the origin of the coordinate axes and a radius of \(1\) unit. So the equation of the unit circle is:

\(\color{blue}{x^2+y^2=1}\)

Note: the above equation satisfies all the points lying on the circle across the four quadrants.

Finding trigonometric functions using a unit circle

Consider a right triangle located in a unit circle on the Cartesian coordinate plane. The radius of the circle represents the hypotenuse of the right triangle. The radius vector makes an angle \(θ\) with the positive \(x\)-axis and the coordinates of the endpoint of the radius vector are \((x, y)\). Here the values of \(x\) and \(y\) are the lengths of the base and the altitude of the right triangle. By applying this to trigonometry, we can find the values of the trigonometric ratio as follows:

\(\color{blue}{sin\:\theta=\frac{Altitude}{Hypoteuse}=\frac{y}{1}}\)

\(\color{blue}{cos\:\theta=\frac{Base}{Hypotenuse}=\frac{x}{1}}\)

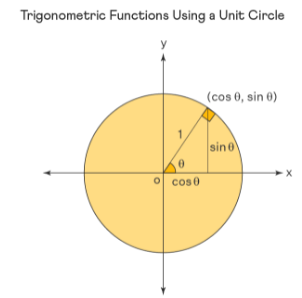
Note: now we have \(sin\:\theta = y\), \(cos\:\theta = x\), and using this, we have \(tan\:\theta = \frac{y}{x}\).

Unit circle and trigonometric identities

For a right triangle placed in a unit circle in the cartesian coordinate plane, with hypotenuse, base, and altitude measuring \(1\), \(x\), \(y\) units respectively, the unit circle identities can be given as:

• \(\color{blue}{sin\:\theta =\frac{y}{1}}\)
• \(\color{blue}{cos\:\theta =\frac{x}{1}}\)
• \(\color{blue}{tan\:\theta =\frac{sin\:\theta }{cos\:\theta }=\frac{y}{x}}\)
• \(\color{blue}{sec\:\left(\theta \right)=\frac{1}{x}}\)
• \(\color{blue}{csc\:\left(\theta \right)=\frac{1}{y}}\)
• \(\color{blue}{cot\:\left(\theta \right)=\frac{cos\:\theta }{sin\:\theta }=\frac{x}{y}}\)

Unit Circle – Example 1:

Does point \(A (\frac{1}{2}, \frac{1}{2})\) lie on the unit circle?

Solution:

The equation of a unit circle is: \(x^2+y^2=1\)

Substituting \(x =\frac{1}{2}\) and \(y = \frac{1}{2}\), we get:

\(=\frac{1}{2}^2+\frac{1}{2}^2\)

\(=\frac{1}{4}+\frac{1}{4}\)

\(=\frac{2}{4}=\frac{1}{2}\)

\(≠ 1\)

Therefore \((\frac{1}{2}, \frac{1}{2})\) doesn’t lie on the unit circle.

Exercises for Unit Circle

Find the value of a function using a unit circle chart.

1. \(\color{blue}{sin\:900^{^{\circ }}}\)
2. \(\color{blue}{cos\:240^{^{\circ }}}\)
3. \(\color{blue}{tan\:225^{^{\circ }}}\)

1. \(\color{blue}{0}\)
2. \(\color{blue}{-\frac{1}{2}}\)
3. \(\color{blue}{1}\)