Long Division using 1 Number
In this article, we are going to teach you the long division and its application and how to do it step by step.

In mathematics, long division is a technique utilized for dividing larger figures into parts or groups.
The long division assists in splitting the division problem into a series of simpler steps.
As with all division problems, a big number called a dividend gets divided via another number, known as the divisor, to provide an answer, known as a quotient, and at times there is a remainder.
There are many different parts involved in an equation using long division:
A dividend is a figure on the righthand side of an equation, underneath the line. It signifies the quantity being divided.
A divisor is a figure on the left-hand side – it is the one that does the dividing.
A quotient is a numeral on the top. This signifies the solution, or the amount of units there are in each of the place values after an equation has been done.
A remainder is a numeral on the top right. This signifies the units that are left which cannot be divided evenly into a quotient.
Related Topics
- Division
- How to Divide Polynomials?
- How to Divide Rational Expressions?
- How to Divide Mixed Numbers?
How is Division done?
Follow these steps here to find out the way division is done:
Step one: Write down the division symbol, then write the divisor on its lefthand side, and the dividend is included underneath that symbol.
Step two: Get the \(1\)st number of the dividend from the left. Then, see if that number is bigger than or equals the divisor. [Should the \(1\)st number of the dividend be lower than the divisor, we reflect on the first \(2\) numbers of the dividend]
Step three: After that divide it via the divisor, then put the result on top as the resulting quotient.
Step four: Subtract the product of the divisor as well as the number placed in the quotient from the \(1\)st number of the dividend and then write down the difference below.
Step five: Bring down the subsequent number of the dividend (if it exists).
Step six: Do all these steps until you come up with the remainder, which is lower than the divisor.
Long Division Hints and Secrets:
The following are several vital hints and secrets to assist one in doing long division:
- When it comes to whole numbers, a dividend is constantly more than or it equals a divisor as well as the quotient.
- A remainder is constantly less than a divisor.
- In division, a divisor can’t be zero.
- The division is repeated subtraction, thus you are able to check the quotient via repetitive subtractions also.
- You can validate both the quotient and remainder of the division utilizing the division formula as follows: \(Dividend = (Divisor × Quotient) + Remainder\).
- Should a remainder be zero, you are able to check the quotient by multiplying it with a divisor. Should a be equal to a dividend, this means the quotient is right.
Long Division using 1 Number – Example 1:
Find the quotient.
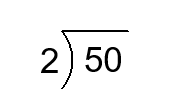
Solution:
\(\frac{50}{2}\) means the number of \(2\) that must be added to get \(50\). In terms of partition, \(\frac{50}{2}\) means the size of each of \(2\) parts into which a set of size \(50\) is divided. For example \(50\) apples divides into \(2\) groups of \(25\) apples.
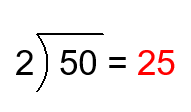
Long Division using 1 Number – Example 2:
Find the quotient.
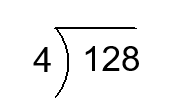
Solution:
\(\frac{128}{4}\) means the number of \(4\) that must be added to get \(128\). In terms of partition, \(\frac{128}{4}\) means the size of each of \(4\) parts into which a set of size \(128\) is divided. The answer is \(32\)
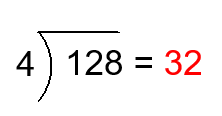
Exercises for Long Division using 1 Number
Find the quotient.
1)
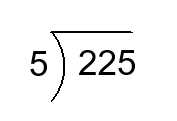
2)
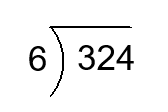

- \(\color{blue}{45}\)
- \(\color{blue}{54}\)
Related to This Article
More math articles
- Measuring Length Change: Definite Integrals in Continuous Growth Analysis
- 10 Most Common ISEE Middle-Level Math Questions
- The Ultimate 6th Grade TCAP Math Course (+FREE Worksheets)
- The Ultimate FTCE General Knowledge Math Course (+FREE Worksheets & Tests)
- The Ultimate Geometry Course
- 3rd Grade MEA Math Worksheets: FREE & Printable
- Top 10 4th Grade ACT Aspire Math Practice Questions
- How to Use Number Lines to Graph Fractions as Decimals
- 8th Grade PSSA Math Worksheets: FREE & Printable
- How to Understand the Properties of Isosceles and Equilateral Triangles

















What people say about "Long Division using 1 Number - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.