How to Solve Venn Diagrams and the Addition Rule?

A Venn diagram is a visual representation of the results of an investigation. It usually consists of a box containing the sample space \(S\), as well as circles or ovals. The events are represented by circles or ovals.

Related Topics

• How to Solve Probability Problems
• How to Solve Multiplication Rule for Probabilities

A step-by-step guide to Venn diagrams and the addition rule

In a probability experiment, if \(A\) and \(B\) are two occurrences, the likelihood that any of them will occur is:

\(\color{blue}{P (A\ or B)=P (A)+P (B)−P (A\ and B)}\)

The Venn diagram shows here as follows:

\(\color{blue}{P (A∪B)=P (A)+P (B)−P (A∩B)}\)

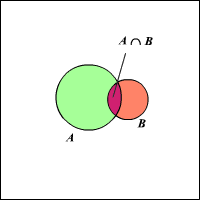
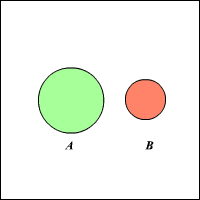
If \(A\) and \(B\) are two mutually exclusive events, \(P(A∩B)=0\). The probability of either of the events occurring is then:

\(\color{blue}{P (A\ or B)=P (A)+P (B)}\)

In a Venn diagram, this might look like this:

\(\color{blue}{P(A∪B)=P(A)+P(B)}\)

Venn Diagrams and the Addition Rule – Example 1:

In a group of \(103\) students, \(32\) are freshmen and \(46\) are sophomores. Find the probability that a student picked from this group at random is either a freshman or sophomore.

First, find the probability of freshman and sophomore:

\(P( freshman)=\frac{32}{103}\)

\(P( sophomores)=\frac{46}{103}\)

Then, use this formula to find the probability of freshman or sophomore: \(\color{blue}{P (A\ or B)=P (A)+P (B)}\)

\(P( freshman\ or sophomore)=\frac{32}{103}+\frac{46}{103}=\frac{32+46}{103}=\frac{78}{103}\).

Venn Diagrams and the Addition Rule – Example 2:

In a group of \(114\) students, \(41\) are juniors, \(50\) are male, and \(23\) are male juniors. Find the probability that a student picked from this group at random is either a junior or male.

First, find the probability of juniors, male and male juniors:

\(P ( juniors)=\frac{41}{114}\)

\(P ( male)=\frac{50}{114}\)

\(P (male juniors)=\frac{23}{114}\)

Then, use this formula to find the probability junior or male: \(\color{blue}{P (A\ or B)=P (A)+P (B)−P (A\ and B)}\)

\(P( junior\ or male )=\frac{41}{114}+\frac{50}{114}-\frac{23}{114}=\frac{(41+50)-23}{114}=\frac{91-23}{114}=\frac{68}{114}\)

Exercises for Venn Diagrams and the Addition Rule

1. We have to draw a card from a well-shuffled \(52\)-card deck. So what is the chance of getting a diamond or a face card?
2. For two events \(A\) and \(B\), \(P(A)= \frac{3}{5}\), \(P(B) = \frac{3}{4}\), and \(P(A∪B) = \frac{5}{6}\). Find the probability of \(A∩B\).
3. A glass jar consists of \(3\) green,\(2\) red, \(3\) blue and \(4\) yellow marbles. If a marble is randomly selected from a jar, how likely is it to be yellow or green?
4. A day of the week is chosen at random. What is the probability of choosing on Sunday or Monday?

1. \(\color{blue}{\frac{11}{26}}\)
2. \(\color{blue}{\frac{31}{60}}\)
3. \(\color{blue}{\frac{7}{12}}\)
4. \(\color{blue}{\frac{2}{7}}\)