How to Solve Double Angle Identities?
A double angle formula is a trigonometric identity that expresses the trigonometric function \(2θ\) in terms of trigonometric functions \(θ\). In this step-by-step guide, you will learn more about double-angle formulas.
[include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
The double angle formulas are used to find the values of double angles of trigonometric functions using their single angle values. Also, the double-angle formulas can be used to derive the triple-angle formulas.
Related Topics
A step-by-step guide to double angle formulas
The double angle formulas are the special cases of the sum formulas of trigonometry and some alternative formulas are derived by using the Pythagorean identities. The sum formulas of trigonometry are:
- \(\color{blue}{sin\:\left(A\:+B\right)=sin\:A\:cos\:B\:+\:cos\:A\:sin\:B}\)
- \(\color{blue}{cos\:\left(A\:+\:B\right)=\:cos\:A\:cos\:B\:-\:sin\:A\:sin\:B}\)
- \(\color{blue}{tan\:\left(A\:+\:B\right)=\:\frac{\left(tan\:A\:+\:tan\:B\right)}{\left(1\:-\:tan\:A\:tan\:B\right)}}\)
What are double-angle formulas?
We derive double-angle formulas of \(sin, cos,\) and \(tan\) by substituting \(A=B\) in each of the above-sum formulas. Also, we will extract some alternative formulas that are derived using Pythagorean identities.
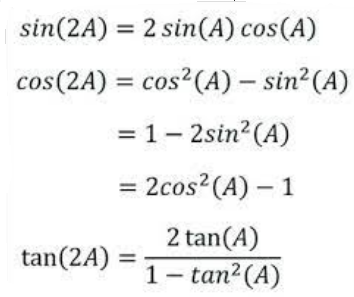
Double Angle Formulas – Example 1:
If \(tan A= \frac{3}{5}\), find the values of \(sin\:2A\).
Solution:
Since the value of \(tan\:A\) is given, we use the double angle formulas for finding \(sin\:2A\).
\(sin\:2A=\frac{2\:tan\:A}{1+tan^2A}\)
\(=\frac{2\left(\frac{3}{5}\right)^2}{1+\left(\frac{3}{5}\right)^2}\)
\(=\frac{\frac{18}{25}}{\frac{34}{25}}\)
\(=\frac{18\times 25}{25\times 34}\)
\(=\frac{9}{17}\)
Exercises for Double Angle Formulas
- Find a formula for \(cos(4x)\) in terms of \(cos x\).
- Solve the equation \(sin\:2x\:=\:cos\:x,\:0\:\le \:x\:<\pi\).
- \(\color{blue}{8\:cos^4x-8\:cos^2x+1}\)
- \(\color{blue}{x=\frac{\pi }{2},\frac{\pi }{6},\frac{5\pi }{6}}\)
Related to This Article
More math articles
- 10 Most Common 5th Grade ACT Aspire Math Questions
- How to Get a Perfect Score of 36 on ACT Math?
- How to Evaluate Decimal Distances on the Map
- SAT Math Practice Test Questions
- Derivatives Demystified: Everything You Need to Know
- Cooking with Fractions: A Guide to Learn How to Adding and Subtracting Fractions in Recipes
- ISEE vs. SSAT
- Ratio, Proportion and Percentages Puzzle – Challenge 30
- ISEE Upper-Level Math Formulas
- Reciprocals
What people say about "How to Solve Double Angle Identities? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.