How to Graph Transformation on the Coordinate Plane: Reflection?
This article teaches you how to graph Reflections on the coordinate plane in a few simple steps.

Step by step guide to graph Transformation: Reflection
- Reflection is flipping an object across a line without changing its size or shape. So, a reflection is a mirror image of the shape. In this case, the image is a reflection of the pre-image and each point of the image is equidistant from each corresponding point in the pre-image.
- Reflecting the image over the \(x\)-axis to create a mirror image is called the reflection on the \(x\)-axis, and in this case, the \(x\)-axis is called the axis of reflection.
- Reflecting the image over the \(y\)-axis to create a mirror image is called the reflection on the \(y\)-axis, and in this case, the \(y\)-axis is called the axis of reflection.
- The reflection of the point \((x, y)\) across the \(x\)-axis is the point \((x, -y)\).
- The reflection of the point \((x, y)\) across the \(y\)-axis is the point \((-x, y)\).
- The reflection of the point \((x, y)\) across the line \(y=x\) is the point \((y, x)\).
- The reflection of the point \((x, y)\) across the line \(y=-x\) is the point \((-y, -x)\).
- When reflecting a point in the origin, both the \(x\)-coordinate and the \(y\)-coordinate is negated.\((x, y)→(-x, -y)\)
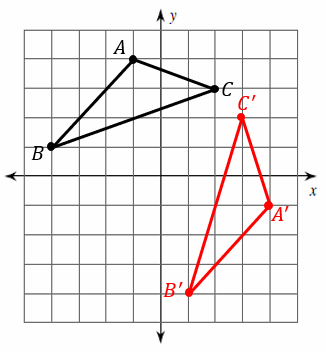
Transformation: Reflection – Example 1:
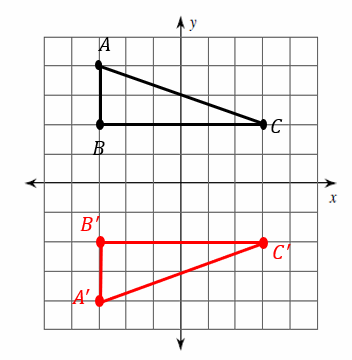
Graph the image of the figure using the transformation given. Reflection across the \(x\)-axis.
Solution:
Find the original coordinates:
\(A=(-3, 4)\) \(B=(-3, 2)\) \(C=(3, 2)\)
The reflection of the point \((x, y)\) across the \(x\)-axis is the point \((x, -y)\), So:
\(A^\prime=(-3, -4)\) \(B^\prime=(-3, -2)\) \(C^\prime=(3, -2)\)
The image of triangle \(ABC\) is \(A^\prime B^\prime C^\prime\) . (the mark \(^\prime\) is called prime.)
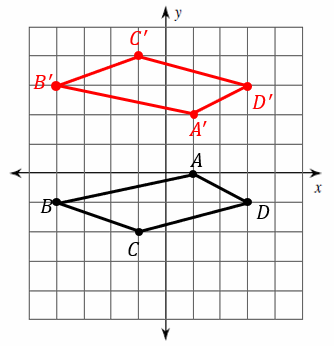
Transformation: Reflection – Example 2:
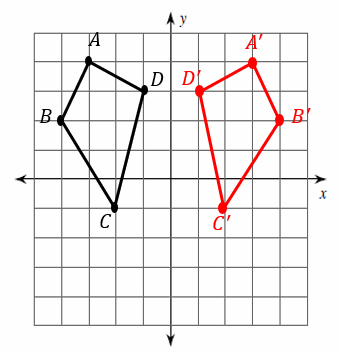
Graph the image of the figure using the transformation given. Reflection across the \(y\)-axis.
Solution:
Find the original coordinates:
\(A=(-3, 4)\) \(B=(-4, 2)\) \(C=(-2, -1)\) \(D=(-1, 3)\)
The reflection of the point \((x, y)\) across the \(y\)-axis is the point \((-x, y)\), So:
\(A^\prime=(3, 4)\) \(B^\prime=(4, 2)\) \(C^\prime=(2, -1)\) \(D^\prime=(1, 3)\)
The image of Polygon \(ABCِِD\) is \(A^\prime B^\prime C^\prime D^\prime\).
Exercises for Transformation: Reflection
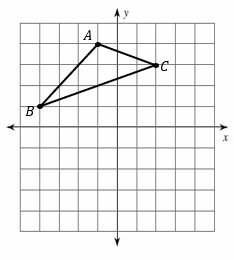
Graph the image of the figure using the transformation given.
1. Reflection across line: \(y=x\)
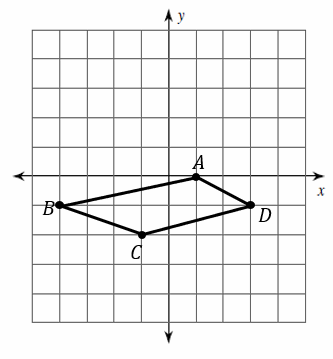
2. Reflection across line: \(y=1\)

Related to This Article
More math articles
- Top 10 Free Websites for PERT Math Preparation
- Overview of Middle-Level SSAT Mathematics Test
- Top 10 Free Websites for GED Math Preparation
- A Comprehensive Look at Average vs Instantaneous Rate of Change
- How to Calculate Segment Lengths in Circles Using the Power Theorem
- PSAT Cаlсulаtоr Pоliсу
- How to Find Missing Angels in Quadrilateral Shapes? (+FREE Worksheet!)
- Vectors Introduction
- Fundamental Theorem of Calculus: A Principle That Saves Your Life
- How to Ace the SHSAT Test?


















What people say about "How to Graph Transformation on the Coordinate Plane: Reflection? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.