How to Graph Inverse of the Tangent Function?

Step-by-step guide to graphing the inverse of the tangent function

Inverse \(tan\) is the inverse of the \(tan\) function and is one of the inverse trigonometric functions. It is mathematically written as \(tan^{-1}x\) or \(atan x\) or \(arctan x\). If two functions \(f\) and \(f^{-1}\) are inverse of each other, then whenever \(f(x) = y\), we have \(x = f^{-1}(y)\). So \(tan x = y ⇒ x = tan^{-1}(y)\). That is, when \(tan\) moves from one side of the equation to the other, it becomes \(tan^{-1}\).

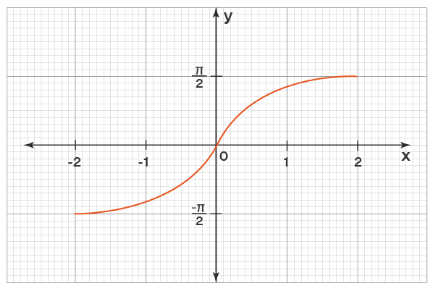
The graph of the inverse tan function with its range as the main branch \((-\frac{π}{2}, \frac{π}{2})\) can be drawn using the table below. Here we have chosen random values of \(x\) in the domain of inverse \(tan x\) which is \(R\).

By plotting these points on the graph, we get the reverse \(tan\) graph.