How to Graph Absolute Value Function?

The absolute value represents the distance of a number on the number line from the origin, better known as zero. The absolute value of a number is never negative. It ignores in which direction from zero the number lies, it only matters how far it is.

Related Topics

• How to Graph Absolute Value Inequalities
• How to Solve an Absolute Value Inequality

A step-by-step guide to graphing absolute value function

Let’s look at the most basic graph of the absolute value function, \(y=|x|\)

Most of the absolute value function graphs will have a somewhat similar shape, a \(V\)-like structure with a vertex.

The following steps will be useful in graphing absolute value functions:

• Step 1: Before plotting any absolute value function, first, we must plot the absolute value parent function:

\(y=|x|\)

Let us take some random values for \(x\).

\(x=−3→y=|−3|=3→(−3,3)\)

\(x=−2→y=|−2|=2→(−2,2)\)

\(x=−1→y=|−1|=1→(−1,1)\)

\(x=0→y=|0|=0→(0,0)\)

\(x=1→y=|1|=1→(1,1)\)

\(x=2→y=|2|=2→(2,2)\)

\(x=3→y=|3|=3→(3,3)\)

If we plot these points on the graph sheet, we will get a graph as given below.

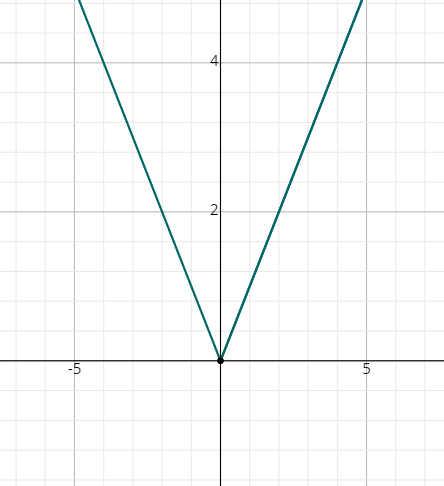
When we look at the above graph, clearly the vertex is \((0, 0)\).

• Step 2: Write the given absolute value function as \(y−k=|x−h|\).
• Step 3: To get the vertex of the absolute value function above, equate \((x – h)\) and \((y – k)\) to zero, that is,

\(x−h=0\) and \(y−k=0\)

\(x=h\) and \(y=k\)

Therefore, the vertex is \((h, k)\).

• Step 4: According to the vertex, we have to shift the above graph.

Note: If we have negative signs in front of absolute signs, we have to flip the curve over.

Graphing Absolute Value Function – Example 1:

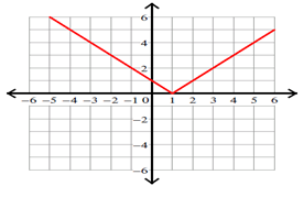
Graphing absolute value function \(y=|x−1|\).

Solution:

The given absolute value function is in the form: \(y−k=|x−h|\)

That is, \(y=|x−1|\)

To get the vertex, equate \((x – 1)\) and \(y\) to zero.

\(x-1=0\) and \(y=0\)

\(x=1\) and \(y=0\)

Therefore, the vertex is \((1,0)\).

So, the absolute value graph of the given function is:

Exercises for Graphing Absolute Value Function

Graph following absolute value function.

• \(\color{blue}{y=\left|x+4\right|+4}\)

• \(\color{blue}{y=-\left|x-2\right|}\)

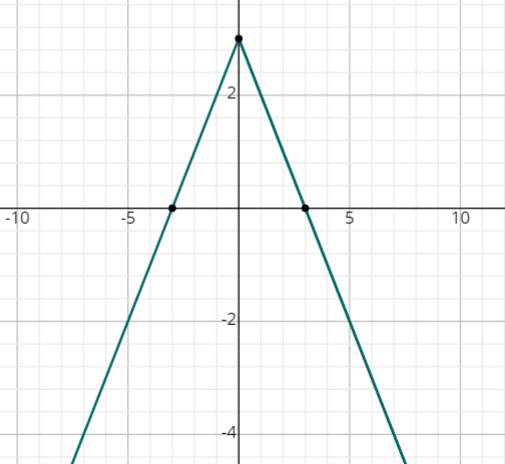
• \(\color{blue}{y=-\left|x\right|+3}\)

• \(\color{blue}{y=\left|x+4\right|+4}\)

• \(\color{blue}{y=-\left|x-2\right|}\)

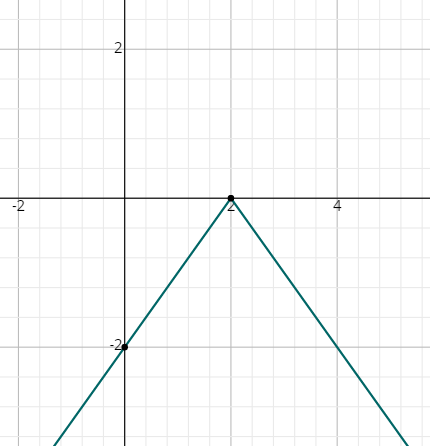
• \(\color{blue}{y=-\left|x\right|+3}\)