How to Find the Surface Area of Spheres?

The formula for the surface area of a sphere depends on the radius and the diameter of the sphere. The surface area of a sphere is always expressed in square units.

Related Topics

• How to Find the Volume of Spheres?

A step-by-step guide to finding the surface area of a sphere

The area that covers the sphere’s outer surface is known as the surface of the sphere. A sphere is a three-dimensional shape of a circle.

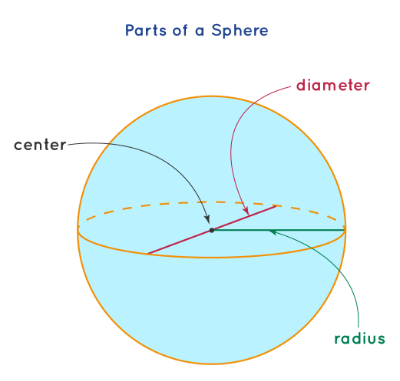
The difference between a sphere and a circle is that a circle is a \(2\)-dimensional shape, while a sphere is a \(3\)-dimensional shape. See the sphere below, which shows the center, radius, and diameter of a sphere.

The formula of the surface area of a sphere

The formula for the surface of the sphere depends on the radius of the sphere. If the radius of the sphere is \(r\) and the surface of the sphere is \(S\). Then, the surface area of the sphere is expressed as follows:

\(\color{blue}{S=4πr^2}\)

In terms of diameter, the surface area of a sphere is expressed as:

\(\color{blue}{S= 4π(\frac{d}{2})^2}\)

where \(d\) is the diameter of the sphere.

How to calculate the surface area of a sphere?

The surface area of a sphere is the space occupied by its surface. We can calculate the sphere surface using the sphere surface area formula. The steps we can use to calculate the surface area of a sphere are:

Let’s give an example to learn how to calculate the surface area of a sphere using its formula.

Example: Find the surface area of a spherical ball that has a radius of \(8\) inches.

Solution:

• Step 1: Note the radius of the sphere. Here, the radius of the ball is \(8\) inches.
• Step 2: As we know, the surface area of sphere \(= 4πr^2\), so after replacing the value of \(r = 8\), we get, the surface area of sphere \(= 4πr^2 = 4 × 3.14 × 8^2 = 4 × 3.14 × 64 = 803.84\)
• Step 3: Therefore, the surface area of the sphere is \(803.84\space in^2\)

Finding the Surface Area of Spheres – Example 1:

If the radius of a sphere is \(25\) \(cm\), find its surface area. 

Solution: 

Given, that the radius \(r\) of the sphere \(= 25\) \(cm\).

The surface area of the sphere \(= 4\pi r^2=\:4×3.14×25^2=4×3.14×625= 7,850\space cm^2\)

Exercises for Finding the Surface Area of Spheres

Find the surface area of each sphere. \((π=3.14)\)

1. \(\color{blue}{ r= 4.5\space ft}\)
2. \(\color{blue}{d=13 \space in}\)
3. \(\color{blue}{r=22 \space cm}\)
4. \(\color{blue}{d=39 \space ft}\)

1. \(\color{blue}{254.34\space ft^2}\)
2. \(\color{blue}{530.66 \space in^2}\)
3. \(\color{blue}{6,079.04 \space cm^2}\)
4. \(\color{blue}{4,775.94 \space ft^2}\)