How to Divide Polynomials?

Dividing polynomials is an operation in which a polynomial is divided by another polynomial, usually to a lesser degree as compared to the dividend. Dividing two polynomials may or may not lead to polynomials.

Related Topics

• The Remainder Theorem

A step-by-step guide to dividing polynomials

Polynomials are algebraic expressions made up of variables and coefficients. The phrase with the highest degree is placed first, followed by the lower terms.

Polynomial division is an algorithm for solving a rational number that represents a polynomial divided by a monomial or another polynomial. The divisor and the dividend are the same as we do for regular division.

Dividing polynomials by monomials

When dividing polynomials by monomials, the division can be done in two ways:

Splitting the terms method:

Split the terms of the polynomial separated by the operator (+) or (-) between them and simplify each sentence.

Factorization method:

When dividing polynomials, you may have to factor in polynomials to find a common factor between the numerator and the denominator.

Dividing polynomials using long division

Let’s review the algorithm for dividing polynomials by binomials using an example:

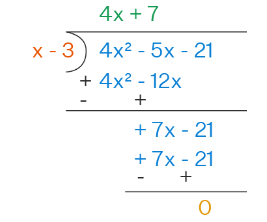
1. Divide the first term of the dividend ((4x^2)) by the first term of the divisor ((x)) and place it as the first term in the quotient ((4x)).
2.  Multiply the divisor by that answer, and place the product ((4x^2- 12x)) below the dividend.
3. Subtract to create a new polynomial ((7x-21)).
4. Repeat the same process with the new polynomial after subtraction.

So, when divide a polynomial ((4x^2 – 5x – 21)) with a binomial ((x – 3)), the quotient is (4x+7) and the remainder is (0).

Dividing polynomials using synthetic division

Synthetic division is a technique for dividing a polynomial by a linear binomial by considering only the values of the coefficients. In this method, we first write polynomials in standard form, including the highest degree to the lowest degree.

When writing with descending powers, use (0) as the coefficient of the missing phrases. For example, (x^3+3) has to be written as (x^3+ 0x^2+ 0x + 3).

Follow these steps to divide a polynomial using the synthetic division method:

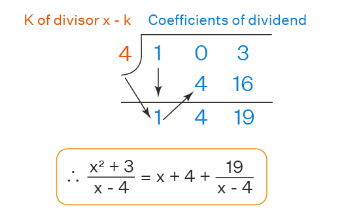
Let us divide (x^2+ 3) by (x – 4).

1. Write the divisor in the form of (x – k) and write (k) on the left side of the division. Here, the divisor is (x-4), so the value of (k) is (4).
2. Adjust the division by writing the dividend coefficients on the right and (k ) on the left.
3. Now, bring down the coefficient of the highest degree term of the dividend as it is. Here, the leading coefficient is (1) (coefficient of (x^2)).
4. Multiply (k) by that leading coefficient and write the product below the second coefficient to the left side of the dividend. So, we get, (4×1=4) that we will write below (0).
5. Add the numbers written in the second column. So, we get, (0+4=4).
6. Repeat the same multiplication process (k) with the number obtained in step five and write the product in the next column to the right.
7. Finally, we write the final answer, which will be one degree less than the dividend. So, in our dividends, the highest degree is (x^2), so in the quotient, the highest degree term will be (x). Therefore, the answer is obtained (x+4+frac{19}{x-4}).

Exercises for Dividing Polynomials

Divide.

1. (color{blue}{left(2x^2-5x-3right)div left(x-3right)})
2. (color{blue}{left(2x^{^6}−5x^{^5}−4x^{^4}+10x^{^3}+6x^{^2}−17x+5right)div left(2x−5right)})
3. (color{blue}{:8x^6+4x^5−14x^4−5x^3+x^2−2xdiv 2x+1})
4. (color{blue}{frac{27m^6+9m^4−81m^2}{9m^2}})

1. (color{blue}{2x+1})
2. (color{blue}{x^5-2x^3+3x-1})
3. (color{blue}{4x^5-7x^3+x^2-1+frac{1}{2x+1}})
4. (color{blue}{3m^4+m^2-9})

Recommended EffortlessMath Books

For a workbook that walks through polynomial division with both long division and synthetic division, the Algebra II for Beginners covers the full unit with worked examples. For pre-calc-level coverage that connects polynomial division to rational functions and partial fractions, see the Pre-Calculus for Beginners.

Algebra II for Beginners 2027 The Ultimate Step by Step Guide to Acing Algebra II

Download

$27.99 Original price was: $27.99.$17.99Current price is: $17.99.

Rated 5.00 out of 5 based on 1 customer rating

Satisfied 1 Students

Frequently Asked Questions

How do you divide polynomials using long division?

Follow the same cycle as number long division: divide, multiply, subtract, bring down. Divide the leading term of the dividend by the leading term of the divisor, multiply the whole divisor by that result, subtract, and repeat. For (x² + 5x + 6) ÷ (x + 2), x² ÷ x = x, and after subtracting x² + 2x you are left with 3x + 6, giving a quotient of x + 3.

How do you divide polynomials using synthetic division?

Synthetic division works when the divisor looks like x − c. Write c and the dividend’s coefficients, bring down the first one, multiply by c, add to the next coefficient, and repeat. For (x³ − 2x² − 5x + 6) ÷ (x − 3), the coefficients 1, −2, −5, 6 become 1, 1, −2 with remainder 0, so the quotient is x² + x − 2.

How do you divide polynomials by monomials?

Split the polynomial and divide each term by the monomial separately, dividing the coefficients and subtracting the exponents. For example, (6x³ − 9x² + 3x) ÷ 3x = 2x² − 3x + 1. Watch the signs on each term, and remember that 3x ÷ 3x is 1, not 0.

What is the easiest way to divide polynomials?

If the divisor is a monomial, divide term by term. If it is a linear binomial like x − 4, synthetic division is the fastest. For any other divisor, such as x² + 1, use long division. Before choosing, check whether the dividend factors, because a shared factor can cancel and save you the whole process.

How do you divide polynomials without long division?

Try factoring first. For (x² − 9) ÷ (x − 3), factor the top into (x − 3)(x + 3) and cancel, leaving x + 3. When the divisor is x − c, synthetic division is another shortcut, and if you only need the remainder, the Remainder Theorem says it equals f(c), so you can just substitute c.

What is polynomial division used for?

Polynomial division helps you factor higher-degree polynomials, find the remaining zeros once one zero is known, and simplify rational expressions. For example, if x = 1 is a root of x³ − 7x + 6, dividing by x − 1 gives x² + x − 6, which factors as (x + 3)(x − 2), so the other roots are −3 and 2.

Related EffortlessMath Lessons

If a topic on this page feels rusty, these short lessons go deeper:

• The Remainder Theorem
• How to use synthetic division (resource currently unavailable)
• Factoring polynomials (resource currently unavailable)
• Rules of exponents
• Order of operations (PEMDAS)