Full-Length DAT Quantitative Reasoning Practice Test

Taking a Full-length DAT Quantitative Reasoning practice test is the best way to help you get familiar with the test format and feel more confident. Not only will this help you measure your exam readiness and solidify the concepts you’ve learned, but it is the best way to simulate test day.
To help you get the best out of this complete and realistic DAT Quantitative Reasoning practice test and prepare your mind and body for the actual test, we recommend that you treat this practice test as a real test. Prepare scratch papers, a pencil, a timer, and a calculator and take the test in one sitting and follow the time limits to the minute.
Take the following full-length DAT Quantitative Reasoning practice test to simulate the test day experience. After you’ve finished, score your tests using the answer keys.
Good luck!

The Absolute Best Book to Ace the DAT Quantitative Reasoning Test

Time to refine your Math skill with a practice test

Take a REAL DAT Quantitative Reasoning test to simulate the test day experience. After you’ve finished, score your test using the answer key.

Before You Start

• You’ll need a pencil, a calculator, and a timer to take the test.
• It’s okay to guess. You won’t lose any points if you’re wrong. So be sure to answer every question.
• After you’ve finished the test, review the answer key to see where you went wrong.
• Calculators are permitted for DAT Quantitative Reasoning Test.
• Use the answer sheet provided to record your answers.
• The DAT Quantitative Reasoning test contains a formula sheet, which displays formulas relating to geometric measurement and certain algebra concepts. Formulas are provided to test- takers so that they may focus on application, rather than the memorization, of formulas.
• For each multiple-choice question, there are five possible answers. Choose which one is best.

Good Luck!

Best DAT Quantitative Reasoning Prep Resource for 2022

DAT Quantitative Reasoning Practice Test

40 questions
Total time for this section: 45 Minutes
You may use a basic calculator for this test.

1- What is the value of \(y\) in the following system of equation?
\(2x+y=7\)
\(4x-2y= 18\)

A. \(-1\)

B. \(-2\)

C. \(1\)

D. \(2\)

E. \(4\)

2- The number 6.45 is 100 times greater than which of the following numbers?

A. 64.5

B. 0.645

C. 0.0645

D.  0.00645

E.  0.000645

3- How many tiles of 12 \(cm^2\) is needed to cover a floor of dimension 6 cm by 32 \(cm\)?

A. 9

B. 12

C. 16

D. 19

E. 24

4- What is the area of a square whose diagonal is 12 cm?

A. 12 \(cm^2\)

B. 34 \(cm^2\)

C. 38 \(cm^2\)

D. 48 \(cm^2\)

E. 72 \(cm^2\)

5- What is the value of \(x\) in the following figure?

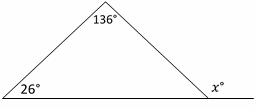
A. 110

B. 125

C. 138

D. 152

E. 162

6- Right triangle ABC is shown below. Which of the following is true for all possible values of angle A and B?

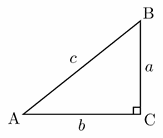
A. \(tan A = tan B\)

B. \(sin A = cos B\)

C. \(tan^2 A=tan^2 B\)

D. \(tan A=1\)

E. \(cot⁡A = sinB\)

7- The marked price of a computer is D dollar. Its price decreased by \(15\%\) in January and later increased by \(22\%\) in February. What is the final price of the computer in D dollars?

A. 0.85 D

B. 0.88 D

C. 0.90 D

D. 0.95 D

E. 1.037 D

8- A bag contains 15 balls: two green, three black, four blue, two brown, a red, and three white. If 14 balls are removed from the bag at random, what is the probability that a red ball has been removed?

A. \(\frac{1}{4}\)

B. \(\frac{1}{6}\)

C. \(\frac{1}{14}\)

D. \(\frac{14}{15}\)

E. \(\frac{15}{14}\)

9- From the figure, which of the following must be true? (figure not drawn to scale)

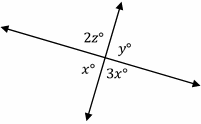
A. \(2y=z\)

B. \(y=x\)

C. \(x≥y\)

D. \(2z=y-2x\)

E. \(z>y\)

10- When \(45\%\) of 30 is added to \(15\%\) of 420, the resulting number is:

A. 57

B. 63

C. 76.5

D. 95.5

E. 110

11- A chemical solution contains \(12\%\) alcohol. If there is 48 ml of alcohol, what is the volume of the solution?

A. 280 ml

B. 360 ml

C. 400 ml

D. 620 ml

E. 780 ml

12- Which of the following points lies on the line \(3x-2y=8\)?

A. \((-3,2)\)

B. \((-1,2)\)

C. \((1,2)\)

D. \((2,-1)\)

E. \((3,0)\) 

13- In the following figure, ABCD is a rectangle, and E and F are points on AD and DC, respectively. The area of ∆BED is 21, and the area of ∆BDF is 32. What is the perimeter of the rectangle?

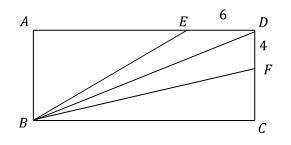
A. 34

B. 46

C. 58

D. 62

E. 74

14- What is the solution of the following inequality?
\(|x+8|≤2\)

A. \(x≥-6 ∪ x≤-10\)

B. \(-10≤x≤-6\)

C. \(x≥-6\)

D. \(x≤-10\)

E. Set of real numbers

15- How long does a 564–miles trip take moving at 60 miles per hour (mph)?

A. 6 hours

B. 7 hours and 30 minutes

C. 8 hours and 45 minutes

D. 9 hours and 24 minutes

E. 12 hours and 15 minutes

16- If a tree casts a 36–foot shadow at the same time that a 3 feet yardstick casts a 4–foot shadow, what is the height of the tree?

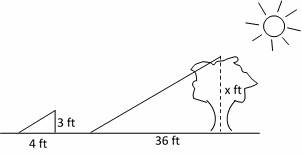
A. 23 ft

B. 27 ft

C. 32 ft

D. 36 ft

E. 44 ft

17- If \(tan \theta = \frac{8}{15}\) and \(sin \theta > 0\), then \(cos \theta =\) ?

A. \(-\frac{15}{17}\)

B. \(-\frac{8}{15}\)

C. \(\frac{8}{17}\)

D. \(\frac{15}{17}\)

E. \(1\)

18- If \(65\%\) of a class are girls, and \(20\%\) of girls play tennis, what percent of the class play tennis?

A. \(9\%\)

B. \(11\%\)

C. \(13\%\)

D. \(15\%\)

E. \(18\%\)

19- In four successive hours, a car travels 55 km, 62 km, 44 km, and 63 km. In the next four hours, it travels with an average speed of 65 km per hour. Find the total distance the car traveled in 8 hours.

A. 368 km

B. 484 km

C. 512 km

D. 625 km

E. 810 km

20- From last year, the price of gasoline has increased from $1.3 per gallon to $1.82 per gallon. The new price is what percent of the original price?

A. \(95\%\)

B. \(110\%\)

C. \(120\%\)

D. \(140\%\)

E. \(160\%\)

21- If \(\frac{5x}{18}=\frac{x-2}{3}\), \(x = ?\)

A. \(\frac{9}{4}\)

B. \(\frac{18}{5}\)

C. \(6\)

D. \(8\)

E. \(12\)

22- A ladder leans against a wall forming a \(60^\circ\) angle between the ground and the ladder. If the bottom of the ladder is 20 feet away from the wall, how long is the ladder?

A. 10 feet

B. 15 feet

C. 20 feet

D. 25 feet

E. 40 feet

23- A rope weighs 732 grams per meter in length. What is the weight in kilograms of 14 meters of this rope? (1 kilograms = 1000 grams)

A. 0.010248

B. 0.10248

C. 1.0248

D. 10.248

E. 102.48

24- In the \(xy\)-plane, the point \((2,-6)\) and \((4,2)\) are on line A. Which of the following equations of lines is parallel to line A?

A. \(y=-2x\)

B. \(y=x\)

C. \(y=\frac{x}{4}\)

D. \(y=2x\)

E. \(y=4x\)

25- When pointing A \((-4,5)\) is reflected over the \(y\)-axis to get point B, what are the coordinates of point B?

A. \((-4,-5)\)

B. \((-4,5)\)

C. \((0,5)\)

D. \((4,-5)\)

E. \((4,5)\)

26- If the area of trapezoid is 42, what is the perimeter of the trapezoid?

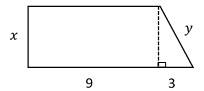
A. 18

B. 24

C. 30

D. 36

E. 42

27- A number is chosen at random from 1 to 18. Find the probability of not selecting a composite number.

A. \(\frac{2}{9}\)

B. \(\frac{3}{8}\)

C. \(\frac{4}{9}\)

D. \(\frac{1}{2}\)

E. \(1\)

28- Removing which of the following numbers will change the average of the numbers to 7 ? 2, 4, 6, 8, 12

A. 2

B. 4

C. 6

D. 8

E. 12

29- If \(50\%\) of \(x\) equal to \(20\%\) of \(30\), then what is the value of \((x-4)^2\)?

A. 48

B. 64

C. 88

D. 128

E. 165

30- \(12\) is \(4\%\) of what number?

A. 30

B. 100

C. 150

D. 300

E. 350

31- If \(f(x)=2x^2-x\) and \(g(x)=x^2-6\), then find \((f-g)(x)\)?

A. \(-x^2-x –6\)

B. \(-x^2–3x+6\)

C. \(x^2–x+6\)

D. \(x^2–3x+6\)

E. \(x^2-3x-6\)

32- If \(f(x)=-x^3-4x^2+6x+7\) and \(g(x)=-1\), what is the value of \(f(g(x))\)?

A. \(-2\)

B. \(-1\)

C. \(0\)

D. \(1\)

E. \(2\)

33- In the following equation when \(z\) is divided by 5, what is the effect on \(x\)?

\(x=\frac{8y+\frac{r}{r+1}}{\frac{6}{z}}\)

A. \(x\) is divided by \(5\)

B. \(x\) is divided by \(10\)

C. \(x\) does not change

D.  \(x\) is multiplied by \(5\)

E.  \(x\) is multiplied by \(10\)

34- A boat sails 35 miles south and then 12 miles east. How far is the boat from its start point?

A. 25 miles

B. 25 miles

C. 59 miles

D. 68 miles

E. 82 miles

35- If \(y=ab^2-3a^2 b\), what is \(y\) when \(a=2\) and \(b=-2\) ?

A. \(-32\)

B. \(-16\)

C. \(16\)

D. \(32\)

E. \(36\)

36- If \(|a|< 1\), then which of the following is true? (\(b > 0\))?
I. \(–b<ba <b\)
II. \(-a < a^2 < a\) if \(a < 0\)
III. \(-2<4a-5<3\)

A. I only

B. II only

C. I and III only

D. III only

E. I, II and III

37- 8 liters of water are poured into an aquarium that’s 16 cm long, 5 cm wide, and 120 cm high. How many cm will the water level in the aquarium rise due to this added water? (1 liter of water = 1000 \(cm^3\))

A. 60

B. 80

C. 100

D. 120

E. 140

38- If a box contains red and blue balls in the ratio of \(3: 4\), how many red balls are there if 120 blue balls are in the box?

A. 30

B. 45

C. 60

D. 75

E. 90

39- If the cotangent of an angle \(β\) is 1, then the tangent of angle \(β\) is

A. \(-1\)

B. \(0\)

C. \(1\)

D. \(2\)

E. \(3\)

40- What is the surface area of the cylinder below?

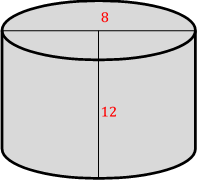
A. 46 π \(in^2\)

B. 58 π \(in^2\)

C. 64 π \(in^2\)

D. 95 π \(in^2\)

E. 128 π \(in^2\)

The Best Books to Ace the DAT Math Test

Answers and Explanations