Full-Length 6th Grade ACT Aspire Math Practice Test-Answers and Explanations

Did you take the 6th Grade ACT Aspire Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
6th Grade ACT Aspire Math Practice Test Answers and Explanations
1- Choice B is correct
Plug in the value of \(x\) and \(y\) and use order of operations rule. \(x=2\) and \(y=-3\)
\(5(4x-3y)-7y^2=5(4(2)-3(-3))-7(-3)^2=5(8+9)-7(9)=5(17)-63=85-63=22\)
2- Choice C is correct
For one hour he earns $18, then for t hours he earns $18t. If he wants to earn at least $78, therefore, the number of working hours multiplied by 18 must be equal to 78 or more than 78.
\(18t≥78\)
3- Choice B is correct
\((108-(3×9))÷9=9^3÷81=9\)
4- Choice B is correct
The ratio of boys to girls is \(3∶ 5\). Therefore, there are 3 boys out of 8 students. To find the answer, first, divide the total number of students by 8, then multiply the result by 3.
\(240÷8=30 ⇒ 30×3=90\)
5- Choice A is correct
Probability\(=\frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}=\frac{9}{9+15+14+16}=\frac{9}{54}\frac{1}{6}=0.16\)
6- Choice D is correct
Let’s compare each fraction: \(\frac{2}{3}<\frac{3}{4}<\frac{7}{9}<\frac{4}{5}\) Only choice D provides the right order.
7- Choice B is correct
Let \(y\) be the width of the rectangle. Then; \(14×y=84→y=\frac{84}{16}=6\)
8- Choice B is correct
\(4×\frac{5}{16}=\frac{20}{16}=1.25\)
A. \(1.25>2\)
B. \(1<1.25<2\) This is the answer!
C. \(\frac{3}{8}=1.25\)
D. \(1.25=2^2\)
9- Choice B is correct
In any rectangle, The measure of the sum of all the angles equals \(180^\circ\).
10- Choice C is correct
\(\frac{824}{17}=48.5\)
The Absolute Best Book to Ace the 6th Grade ACT Aspire Math Test
ACT Aspire Grade 6 Mathematics A Comprehensive Review and Ultimate Guide to the ACT Aspire Math Test
11- Choice B is correct
The area of the trapezoid is: Area \(=\frac{base \space 1+base \space 2}{2}×height=\frac{12+10}{2}x=A→ 11x=A→x=\frac{A}{11}\)
12- Choice B is correct
\(\frac{72}{8}=9, \frac{648}{72}=9, \frac{5,832}{648}=9\), Therefore, the factor is 9.
13- Choice C is correct
Simplify each option provided.
A. \(13-(3×6)+(7×(-6))=13-18+(-42)=-5-42=-47\)
B. \((\frac{25}{400})+(\frac{7}{50})=\frac{25}{400}+\frac{56}{400}=\frac{81}{400}\)
C. \(((22×\frac{30}{6})-(7×\frac{144}{12}))×\frac{18}{2}=(110-84)×9=26×9=234\) (this is the answer)
D. \((\frac{6}{24}+\frac{12}{33})-50=(\frac{1}{4}+\frac{1}{3})-50=(\frac{3}{12}+\frac{4}{12})-50=\frac{7}{12}-50=\frac{-593}{15}\)
14- Choice D is correct
To find the discount, multiply the number (\(100\%\)- rate of discount)
Therefore; \(450(100\%-16\%)=450(1-0.16)=450-(450×0.16)\)
15- Choice A is correct
1,400 out of 11,900 equals to \(\frac{1,400}{11,900}=\frac{200}{1,700}=\frac{2}{17}\)
16- Choice C is correct
The opposite of Nicolas’s integer is \(25\). So, the integer is \(-25\). The absolute value of \(25\) is also \(25\).
17- Choice C is correct
1 yard = 3 feet, Therefore, \(33,759 ft×\frac{1 \space yd}{3 \space ft}=11,253\) yd
18- Choice B is correct
\(16\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(16\%\) of \(x=38\) ml ⇒ \(0.16x=38 ⇒ x=38÷0.16=237.5\)
19- Choice C is correct
\((-2)(9x-8)=(-2)(9x)+(-2)(-8)=-18x+16\)
20- Choice D is correct
1 pt = 16 fluid ounces. \(576÷16=36\)
Then: 576 fluid ounces = 36 pt
21- Choice D is correct
1 kg = 1000 g and 1 g = 1000 mg,
120 kg = 120 × 1000 g = 120 × 1000 × 1000 = 120,000,000 mg
22- Choice C is correct
The diameter of a circle is twice the radius. Radius of the circle is \(\frac{14}{2}=7\).
Area of a circle \(= πr^2=π(7)^2=49π=49×3.14=153.86≅153.9\)
23- Choice B is correct
Average (mean) \(=\frac{sum \space of \space terms}{number \space of \space terms}=\frac{15+17+12+16+21+23}{6}=\frac{104}{6}=17.33\)
24- Choice C is correct
Prime factorizing of \(18=2×3×3\), Prime factorizing of \(24=2×2×2×3\)
LCM \(= 2×2×2×3×3=72\)
25- Choice B is correct
The coordinate plane has two axes. The vertical line is called the \(y\)-axis and the horizontal is called the \(x\)-axis. The points on the coordinate plane are addressed using the form \((x,y)\). Point A is one unit on the left side of the \(x\)-axis, therefore its \(x\) value is 4 and it is two units up, therefore its \(y\) axis is 2. The coordinate of the point is: (4, 2)
Best 6th Grade ACT Aspire Math Prep Resource for 2022
26- Choice B is correct
\(α\) and \(β\) are supplementary angles. The sum of supplementary angles is 180 degrees.
\(α+β=180^\circ→α=180^\circ-β=180^\circ-125^\circ=55^\circ,\) Then, \(\frac{α}{β}=\frac{55}{125}=\frac{11}{25}\)
27- Choice C is correct
Opposite number of any number \(x\) is a number that if added to \(x\), the result is 0. Then:
\(7+(-7)=0\) and \(4+(-4)=0\)
28- Choice D is correct
\(-5<2x+7≤3\)→ (add (\(-7\))all sides) \((-7)+(-5)<2x+7+(-7)≤3+(-7) \) →\(-12<2x≤-4\)→(divide all sides by 2),\(-6<x≤-2\)
In inequality \(-6<x≤-2\), \(x\) is fewer or equal to \(-2\) and more than \(-6\). Only choice D represents the same inequality on the number line.
29- Choice B is correct
A. Number of books sold in April is: \(690\)
Number of books sold in July is: \(1,150→ \frac{690}{1,150}≠2\)
B. Number of books sold in July is: \(1,150\)
Half the number of books sold in May is: \(\frac{1,150}{2}=575→690>575\) (it’s correct)
C. Number of books sold in June is: \(375\)
Half the number of books sold in April is: \(\frac{690}{3}=230→240<375\)
D. \(690+375=1,065>1,150\)
30- Choice B is correct
\(51∶18=17∶6, 17×3=51\) and \(8×3=18\)
31- The answer is 175.
\(-60=115-x\); First, subtract 115 from both sides of the equation. Then:
\(-60-115=115-115-x→-175=-x\), Multiply both sides by (\(-1\)):
→\(x=175\)
32- The answer is 340.
The ratio of boys to girls is \(4: 5\). Therefore, there are 4 boys out of 9 students. To find the answer, first, divide the total number of students by 9, then multiply the result by 4.
\(765 ÷ 9 = 85 ⇒ 85 × 4 = 340\)
33- The answer is 43.
Plug in the value of \(x\) and \(y\) and use order of operations rule. \(x=2\) and \(y=-1\)
\(6(2x-3y)+(3-2x)^2=6(2(2)-3(-1))+(3-2(2))^2=6(4+3)+(-1)^2 = 42+1=43\)
34- The answer is 30.7.
\(\frac{215}{7}≅30.71≅30.7\)
35- The answer is 378.
Volume of a box \(= ength×width×height=6×7×9=378\)
36- The answer is 6.
Let y be the width of the rectangle. Then; \(15×y=90→y=\frac{90}{15}=6\)
37- The answer is 7.
\(420=2^2×3^1×5^1×7^1\)
38- The answer is 13.
\(\frac{104}{8}=13, \frac{1,352}{104}=13, \frac{17,576}{1,352}=13\)
Therefore, the factor is 13
39- The answer is 1,256.
1 yard = 3 feet
Therefore, \(3,768 ft.×\frac{1 \space yd}{3 \space ft}=1,256 \space yd\)
40- The answer is 60.
Prime factorizing of \(20=2×2×5\)
Prime factorizing of \(12=2×2×3\)
LCM \(=2×2×3×5=60\)
41- The answer is 491.
The diameter of a circle is twice the radius. Radius of the circle is \(\frac{25}{2}\).
Area of a circle \(= πr^2=π(\frac{25}{2})^2=156.25π=156.25×3.14=490.625≅491\)
42- The answer is 13.5.
Average (mean) \(= \frac{sum \space of \space terms}{number \space of \space terms}=\frac{10+11+15+14+15+17+12.5}{7}=13.5\)
43- The answer is 70.
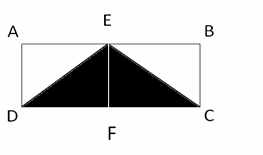
Since E is the midpoint of AB, then the area of all triangles DAE, DEF, CFE, and CBE are equal.
Let x be the area of one of the triangles, then:
\(4x=140→x=35\)
The area of DEC \(=2x=2(35)=70\)
44- The answer is 8.
The perimeter of a rectangle is: \(2×(4+7)=2×11=22\)
The perimeter of circle is: \(2πr=2×3×\frac{10}{2}=30\)
The difference in the perimeter is: \(30-22=8\)
45- The answer is 30.
Find the difference of each pair of numbers:
2, 3, 5, 8, 12, 17, 23, _, 38
The difference of 2 and 3 is 1, 3 and 5 is 2, 5 and 8 is 3, 8 and 12 is 4, 12 and 17 is 5, 17 and 23 is 6, 23 and next number should be 7. The number is 23 + 7 = 30
46- The answer is \(-122\).
Use PEMDAS (order of operation):
\([6 × (–24) + 8] – (–4) + [4 × 5] ÷ 2 = [–144 + 8] – (–4) + [20] ÷ 2 = [–144 + 8] – (–4) + 10 =
[–136] – (–4) + 10 = [–136] + 4 + 10 = –122\)
The Best Books to Ace the 6th Grade ACT Aspire Math Test
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
Related to This Article
More math articles
- Area Models Unveiled: How to Divide Unit Fractions by Whole Numbers
- Math Education Trends In Canadian Education System
- What is a Perfect SAT Score?
- How To Get A Perfect Score Of 800 On SAT Math?
- How many questions are on the SAT Test?
- Full-Length ASVAB Math Practice Test
- DAT Quantitative Reasoning Formulas
- Top 10 TSI Math Practice Questions
- Geometry Puzzle – Critical Thinking 19
- Graphical Insights: How to Solve Systems of Non-linear Equations Step-by-Step






What people say about "Full-Length 6th Grade ACT Aspire Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.