Full-Length Accuplacer Math Practice Test

Doing a Full-length Accuplacer Math practice exam is the top method of helping someone familiarize themselves with the exam format and get more self-confident. Not just will that assist them in measuring their readiness to take the test, it also solidifies what they know, and it’s the top method of mimicking exam dates.
To assist one in getting the top results from this comprehensive and realistic Accuplacer Math practice exam and prepare their body and mind to take a real exam, it’s recommended to act like it’s the real exam. Get your calculator, scratch paper, timer, and pencil ready. Take it according to the real timeframe requirements. After you take the following full-length Accuplacer Math practice exam to mimic the exam day experience, get your score by using the correct answer keys.

The Absolute Best Book to Ace the Accuplacer Math Test

Time to refine your Math skill with a practice test

Take a practice Accuplacer Math test to simulate the test day experience. After you’ve finished, score your test using the answer keys.

Before You Start

• You’ll need a pencil and a calculator to take the test.
• For each question, there are four possible answers. Choose which one is best.
• It’s okay to guess. There is no penalty for wrong answers.
• After you’ve finished the test, review the answer key to see where you went wrong.

Good Luck!

Best Accuplacer Math Prep Resource for 2024

Accuplacer Mathematical Practice Test

Section 1: Arithmetic

(No Calculator)
20 questions
Total time for this section: No time limit.
You may NOT use a calculator on this Section.
(On a real Accuplacer test, there is an onscreen calculator to use on some questions.)

1- A taxi driver earns $7 per 1-hour work. If he works 8 hours a day and in 1 hour he uses 1.5-liters petrol with price $1.5 for 1-liter. How much money does he earn in one day?

A. $38

B. $43

C. $52

D. $60

2- What is the value of \(5.12×4.3\)?

A. 17.768

B. 18.08

C. 21.568

D. 22.016

3- \(25\%\) of what number is equal to 85?

A. 11.25

B. 112.50

C. 340

D. 500

4- Which of the following is greater than \(\frac{15}{7}\)?

A. \(\frac{9}{4}\)

B. \(\frac{3}{2}\)

C. \(\frac{3}{4}\)

D. 1.5

5- Which of the following inequalities is true?

A. \(\frac{4}{5}<\frac{11}{15}\)

B. \(\frac{15}{21}<\frac{6}{7}\)

C. \(\frac{4}{5}<\frac{16}{25}\)

D. \(\frac{9}{7}<\frac{4}{7}\)

6- The price of a car was $32,000 in 2014, $24,000 in 2015 and $18,000 in 2016. What is the rate of depreciation of the price of a car per year?

A. \(10\%\)

B. \(15\%\)

C. \(20\%\)

D. \(25\%\)

7- The price of a sofa is decreased by \(13\%\) to $426.3. What was its original price?

A. $420

B. $490

C. $550

D. $600

8- If \(30\%\) of a class are girls, and \(50\%\) of girls play tennis, what percent of the class play tennis?

A. \(10\%\)

B. \(15\%\)

C. \(20\%\)

D. \(40\%\)

9- If \(80\%\) of A is \(40\%\) of B, then B is what percent of A?

A. \(3\%\)

B. \(30\%\)

C. \(200\%\)

D. \(300\%\)

10- Which of the following is closest to 7.025?

A. 5

B. 5.5

C. 6

D. 7

11- How long does a 390–miles trip take moving at 60 miles per hour (mph)?

A. 4 hours

B. 6 hours and 24 minutes

C. 6 hours and 30 minutes

D. 8 hours and 30 minutes

12- Which of the following expressions has the same value as \(\frac{9}{4}×\frac{7}{3}\)?

A. \(\frac{7×3}{6}\)

B. \(\frac{6×7}{8}\)

C. \(\frac{5×6}{4}\)

D. \(\frac{5×3}{4}\)

13- 84 is What percent of 70?

A. \(20\%\)

B. \(25\%\)

C. \(120\%\)

D. \(150\%\)

14- What is the value of \(1.78+3.045+2.007\)?

A. 6.832

B. 6.985

C. 7.832

D. 8.2563

15- A bank is offering \(5.5\%\) simple interest on a savings account. If you deposit $15,000, how much interest will you earn in six years?

A. $360

B. $720

C. $1,800

D. $4,950

16- When 87 is divided by 7, the remainder is the same as when 27 is divided by

A. 2

B. 4

C. 5

D. 7

17- \(\frac{18}{7}-\frac{11}{7}\)= ?

A. 0.3

B. 0.35

C. 0.85

D. 1.00

18- Sophia purchased a sofa for $605.90. The sofa is regularly priced at $730. What was the percent discount Sophia received on the sofa?

A. \(13\%\)

B. \(15\%\)

C. \(17\%\)

D. \(19\%\)

19- A rope weighs 380 grams per meter in length. What is the weight in kilograms of 9.5 meters of this rope? (1 kilograms \(=\) 1000 grams)

A. 0.0361

B. 0.361

C. 3.61

D. 36.10

20- Which of the following lists shows the fractions in order from least to greatest? \(\frac{1}{3}, \frac{4}{5}, \frac{13}{19}, \frac{7}{11}\)

A. \(\frac{7}{11},\frac{1}{3},\frac{13}{19},\frac{4}{5}\)

B. \(\frac{1}{3},\frac{7}{11},\frac{13}{19},\frac{4}{5}\)

C. \(\frac{7}{11},\frac{1}{3},\frac{4}{5},\frac{13}{19}\)

D. \(\frac{13}{19},\frac{7}{11},\frac{1}{3},\frac{4}{5}\)

The Best Books to Ace the Accuplacer Math Test

Section 2: Quantitative Reasoning, Algebra, And Statistics

(No Calculator)
20 questions
Total time for this section: No time limit.
You may NOT use a calculator on this Section.
(On a real Accuplacer test, there is an onscreen calculator to use on some questions.)

21- Right triangle ABC has two legs of lengths 8 cm (AB) and 15 cm (AC). What is the length of the third side (BC)?

A. 16 cm

B. 17 cm

C. 18 cm

D. 19 cm

22- An angle is equal to two-ninths of its supplement. What is the measure of that angle?

A. 20

B. 30

C. 40

D. 50

23- John traveled 210 km in 7 hours and Alice traveled 175 km in 5 hours. What is the ratio of the average speed of John to the average speed of Alice?

A. \(3: 2\)

B. \(6: 7\)

C. \(5: 9\)

D. \(5: 6\)

24- A taxi driver earns $8.5 per 1-hour work. If he works 10 hours a day and in 1 hour he uses 3-liters petrol with the price of $1.5 for 1-liter. How much money does he earn in one day?

A. $40

B. $50

C. $65

D. $70

25- When a number is subtracted from 45 and the difference is divided by that number, the result is 4. What is the value of the number?

A. 2

B. 4

C. 6

D. 9

26- In the \(xy\)-plane, the point \((-3,2)\) and \((2,-8)\) are on line A. Which of the following points could also be on line A? (Select one or more answer choices)

A. \((-1,3)\)

B. \((-2,0)\)

C. \((3,4)\)

D. \((-1,-5)\)

27- The width of a box is one-fourth of its length. The height of the box is one second of its width. If the length of the box is 40 cm, what is the volume of the box?

A. 1500 cm\(^3\)

B. 1800 cm\(^3\)

C. 2000 cm\(^3\)

D. 2400 cm\(^3\)

28- How many possible outfit combinations come from four shirts, fifth slacks, and seven ties?

A. 100

B. 120

C. 130

D. 140

29- If the area of a trapezoid is 300 cm, what is the perimeter of the trapezoid?

A. 72 cm

B. 75 cm

C. 80 cm

D. 85 cm

30- The area of a circle is less than \(121 π\). Which of the following can be the circumference of the circle?

A. \(20 π\)

B. \(24 π\)

C. \(28 π\)

D. \(32 π\)

31- An integer is chosen at random from 5 to 30. Find the probability of not selecting a composite number?

A. \(\frac{1}{5}\)

B. \(\frac{1}{4}\)

C. \(\frac{6}{25}\)

D. \(\frac{8}{25}\)

32- A boat sails 10 miles south and then 24 miles east. How far is the boat from its start point?

A. 18 miles

B. 22 miles

C. 26 miles

D. 30 miles

33- The ratio of boys and girls in a class is 2:5. If there are 56 students in the class, how many more boys should be enrolled to make the ratio 1:1?

A. 16

B. 22

C. 24

D. 32

34- The score of Emma was two-thirds as that of Ava and the score of Mia was twice that of Ava. If the score of Mia was 72, what is the score, Emma?

A. 12

B. 15

C. 24

D. 29

35- three seventh of 21 is equal to \(\frac{3}{5}\) of what number?

A. 15

B. 20

C. 25

D. 30

36- In 1999, the average worker’s income increased by $1,200 per year starting from a $15,000 annual salary. Which equation represents income greater than average? (I = income, \(x\) = number of years after 1999)

A. \(I<1200x-15000\)

B. \(I>1200x-15000\)

C. \(I>1200x+15000\)

D. \(I<1200x+15000\)

37- The average weight of 15 girls in a class is 50 kg and the average weight of 25 boys in the same class is 60 kg. What is the average weight of all the 40 students in that class?

A. 44.85

B. 48.25

C. 52.5

D. 56.25

38- What is the median of these numbers? \(21,15,13,10,18,6,25\)

A. 8

B. 9

C. 13

D. 15

39- The surface area of a cylinder is \(48π cm^2\). If its height is 5 cm, what is the radius of the cylinder?

A. 3 cm

B. 5 cm

C. 7 cm

D. 9 cm

40- The average of six consecutive numbers is 67.5. What is the smallest number?

A. 60

B. 65

C. 70

D. 75

Section 3: Advanced Algebra and Functions

(Calculator)
20 questions
Total time for this section: No time limit.
You may use a calculator in this Section.
(On a real Accuplacer test, there is an onscreen calculator to use on some questions.)

41- If \((ax+3)(bx-4)=-6x^2+2cx-12\) for all values of \(x\) and \(a+b=5\), what are the two possible values for c?

A. 13.5, 21

B. 11, 22

C. 10, 13.5

D. 11 , 13.5

42- If \(f(x)=7x+2(1-x)\) then \(f(3x)=\)?

A. \(20x+6\)

B. \(15x-6\)

C. \(15x+2\)

D. \(27x+2\)

43- A line in the \(xy\)-plane passes through the origin and has a slope of \(\frac{2}{5}\). Which of the following points lies on the line?

A. \((5,1)\)

B. \((4,-1)\)

C. \((9,10)\)

D. \((15,6)\)

44- Which of the following is equivalent to \((4n^2-5n+12)-(3n^2-4n)\)?

A. \(n+4n^2\)

B. \(n^2-n+12\)

C. \(n^2+2n+12\)

D. \(n+2\)

45- If \(3x+2y=0, 3x-4y=6\), which of the following ordered pairs\( (x,y)\) satisfies both equations?

A. \((\frac{2}{3},-1)\)

B. \((5,-4)\)

C. \((4,-4)\)

D. \((\frac{5}{3},-6)\)

46- John buys a pepper plant that is 8 inches tall. With regular watering, the plant grows 5 inches a year. Writing John’s plant’s height as a function of time, what does the \(y\)-intercept represent?

A. The \(y\)-intercept represents the rate of growth of the plant which is 5 inches

B. The \(y\)-intercept represents the starting height of 6 inches

C. The \(y\)-intercept represents the rate of growth of the plant which is 3 inches per year

D. There is no \(y\)-intercept

47- In the \(xy\)-plane, if (1, 2) is a solution to the system of inequalities above, which of the following relationships between a and b must be true?

A. \(a<b\)

B. \(a>b\)

C. \(a=b\)

D. \(a= b+ a\)

48- Which of the following points lies on the line that goes through the points \((1,-5)\) and \((-3,7)\)?

A. \((2,-3)\)

B. \((5,-12)\)

C. \((-4,10)\)

D. \((3,-6)\)

49- Calculate \(f(-4)\) for the following function \(f\).
\(f(x)=2x^2+4x+1\)

A. 16

B. 17

C. 18

D. 19

50- If \(x≠-4\) and \(x≠9\), which of the following is equivalent to \(\frac{1}{\frac{1}{x+4}+\frac{1}{x-9}}\)?

A. \(\frac{(x-9)-(x+4)}{(x-9)+(x+4)}\)

B. \(\frac{(x-9)(x+4)}{(x+4)+(x-9)}\)

C. \(\frac{(x+4)(x-9)}{(x+4)-(x+5)}\)

D. \(\frac{(x+4)+(x-9)}{(x+4)-(x-9)}\)

51- In the \(xy\)-plane, the line determined by the points (2,m) and (m,10) passes through the origin. Which of the following could be the value of m?

A. \(\sqrt{6}\)

B. \(2\sqrt{5}\)

C. \(6\sqrt{2}\)

D. 9

52- Which of the following is an equation of a circle in the \(xy\)-plane with center \((1,-2)\) and a radius with endpoint \((\frac{1}{3},2)\)?

A. \((x-1)^2+(y+2)^2=\frac{148}{9}\)

B. \(x^2+(y+2)^2=\frac{148}{9}\)

C. \((x-1)^2+(y-2)^2=\frac{148}{9}\)

D. \(x^2+(y-2)^2=\frac{148}{9}\)

53- Given a right triangle \(∆\)ABC whose \(n∠B=90^\circ\),sin⁡C\(=\frac{3}{5}\), find cosA?

A. \(-\frac{1}{2}\)

B. \(\frac{1}{2}\)

C. \(\frac{3}{5}\)

D. \(\frac{4}{5}\)

54- What is the equation of the following graph?

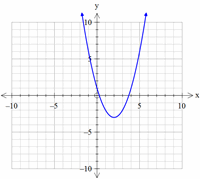
A. \(x^2+6x+5\)

B. \(x^2-3x+1\)

C. \(2x^2-4x+4\)

D. \(x^2-4x+1\)

55- If \(\frac{7}{x}=\frac{21}{(x+4)}\) what is the value of\((-\frac{x}{3}\))?

A. \(-\frac{1}{6}\)

B. \(-\frac{2}{3}\)

C. 1

D. 3

56- A function \(g(6)=8\) and \(g(2)=7\). A function \(f(7)=9\) and \(f(8)=12\). What is the value of \(f(g(6))\)?

A. 5

B. 6

C. 7

D. 12

57- What is the area of the following equilateral triangle if the side AB \(= 14\) cm?

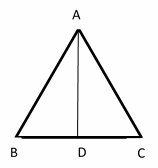
A. \(98\sqrt{3} \)cm\(^2\)

B. \(45\sqrt{3} \)cm\(^2\)

C. \(49\sqrt{3} \)cm\(^2\)

D. \(14\)cm\(^2\)

58- A function \(g(x)\) satisfies \(g(3)=8\) and \(g(4)=10\). A function \(f(x)\) satisfies \(f(8)=12\) and \(f(10)=40\).What is the value of \(f(g(4))\)?

A. 8

B. 10

C. 12

D. 40

59- \(x^2+y^2-6x+4y=4\)
The equation of a circle in the \(xy\)-plane is shown above. What is the radius of the circle?

A. \(\sqrt{17}\)

B. 5

C. \(\sqrt{24}\)

D. \(\sqrt{48}\)

60- Right triangle ABC is shown below. Which of the following is true for all possible values of angle A and B?

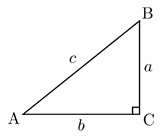
A. tan A \(=\) cot B

B. sin A \(= -\)cos B

C. tan\(^2\) A \(=\) tan\(^2\) B

D. tan A \(= \)1

The Best Books to Ace the Accuplacer Math Test

Answers and Explanations