How to Find Values of Functions from Graphs?
In a few simple steps, we can find the value of the function from the graph. In this step-by-step guide, you will learn more information about finding values of functions from graphs.

A function in mathematics is represented as a rule, which gives a unique output for each input \(x\).
Related Topics
A step-by-step guide to finding values of functions from graphs
We can find the value of the function from the graph in a few simple steps. Note this example to learn how to find a function from a graph. For example, find the value of a function \(f(x)\) when \(x = a\).
- Draw a vertical line through the value \(a\) on the \(x\)-axis.
- Mark the point of intersection of the line \(x = a\) and the graph of \(f(x)\).
- Draw a horizontal line from the point of intersection to the \(y\)-axis.
- Let the horizontal line meet the \(y\)-axis at \(b\).
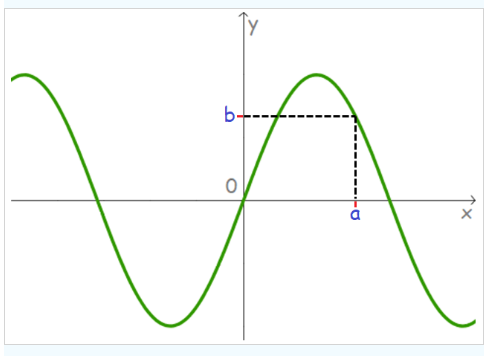
The value of the function \(f(x)\) at \(x = a\) is \(b\). That is, \(f(a) = b\).
Finding Values of Functions from Graphs – Example 1:
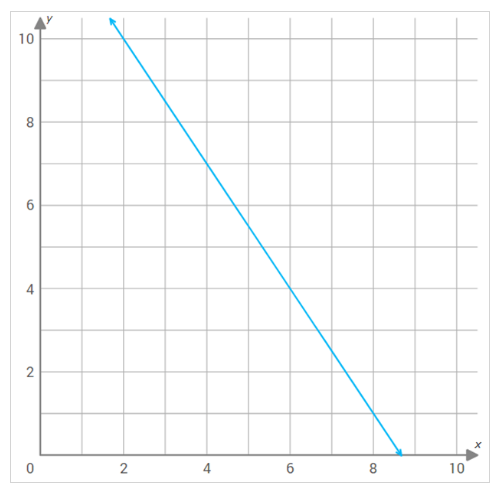
Use the graph of \(f(x)\) shown below to find \(f(4)\).
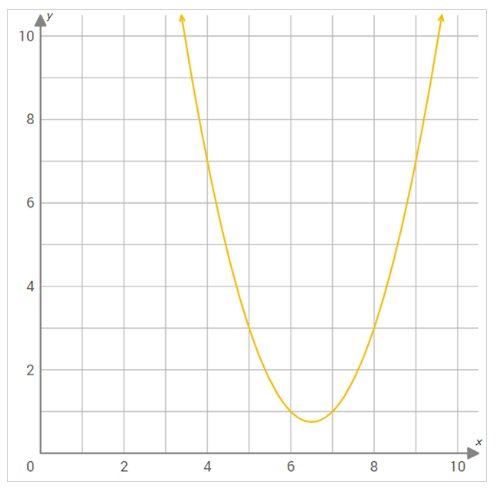
Solution:
First, draw a vertical line through \(4\) on the \(x\)-axis. Then mark the intersection of the vertical line \(x = 4\) and the graph \(f (x)\). Now draw a horizontal line from the point of intersection to the \(y\)-axis.
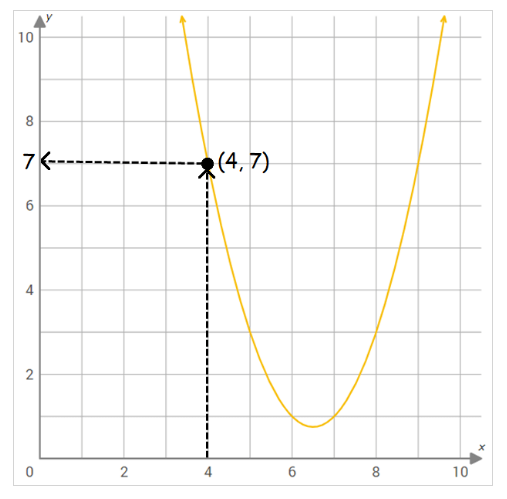
So, the value of the function \(f(x)\) at \(x = 4\) is \(7\).
Exercises for Finding Values of Functions from Graphs
- Use the graph of \(f(x)\) shown to find \(f(8)\).
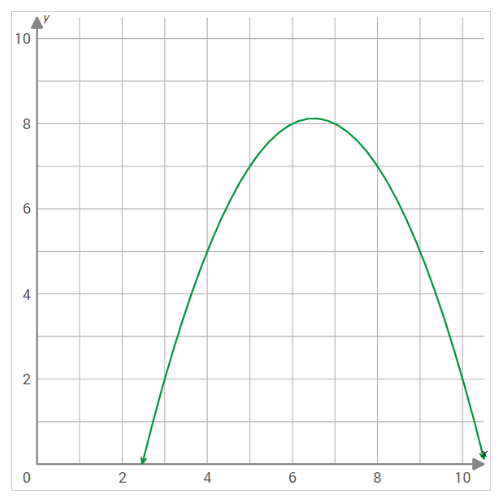
- Use the graph of \(f(x)\) shown to find \(f(2)\).

- \(\color{blue}{7}\)
- \(\color{blue}{10}\)
Related to This Article
More math articles
- Full-Length PSAT 10 Math Practice Test
- How to Solve Word Problems of Volume of Cubes and Rectangular Prisms
- Top 10 Tips to Overcome PSAT Math Anxiety
- The Ultimate 7th Grade MAAP Math Course (+FREE Worksheets)
- How to Identify the Change, Price, or Amount Paid
- How to Calculate Limits of Functions
- 5th Grade CMAS Math Worksheets: FREE & Printable
- 10 Most Common 4th Grade FSA Math Questions
- Number Properties Puzzle -Critical Thinking 2
- 4th Grade IAR Math Worksheets: FREE & Printable


























What people say about "How to Find Values of Functions from Graphs? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.