How to Add Polynomials to Find Perimeter

The sides of two-dimensional figures are sometimes considered polynomials. This article contains instructions for calculating the perimeter of such polygons.
Related Topics
A step-by-step guide to Add Polynomials to Find Perimeter
When the sides of a polygon are given in the polynomial form, you must add the polynomials together to calculate the perimeter of these shapes. To add polynomials, find like terms and add them together.
Adding Polynomials to Find Perimeter -Example 1
If each side of a square is \(2x+3\), what is the perimeter of the square?
Solution:
The perimeter of the square is: Perimeter\(=4(2x+3)\)
Expand the expression and simplify: Perimeter\(=4(2x+3)=8x+12\)
Adding Polynomials to Find Perimeter -Example 2
Find the perimeter. Simplify your answer.
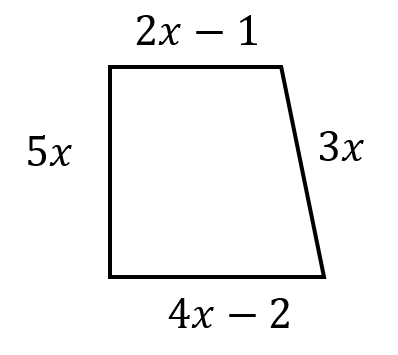
Solution:
The perimeter of the shape is the sum of the sides. So,
Perimeter\(=(2x-1)+(3x)+(5x)+(4x-2)=2x-1+3x+5x+4x-2\)
Group and add like terms,
Perimeter\(=(2x+3x+5x+4x)+(-1-2)=14x-3\)
Exercises for Add Polynomials to Find Perimeter
- If each side of a square is \(3x-4\), what is the perimeter of the square?
- What is the perimeter of a rectangle if the length is \(3x^2-5\) and the width is \(3x+3\)?

- \(\color{blue}{12x-16}\)
- \(\color{blue}{6x^2+6x-4}\)
Related to This Article
More math articles
- What is the Best Algebra Book in the World?
- 4 Best Keyboards for Online Teaching
- Discover the Gateway: “CBEST Math for Beginners” Full Solution Handbook
- 4th Grade PARCC Math Worksheets: FREE & Printable
- Overview of the CHSPE Mathematics Test
- ACT Math- Test Day Tips
- How to Find Slope? (+FREE Worksheet!)
- 8th Grade SBAC Math Practice Test Questions
- How to Verify Inverse Functions by Composition?
- Top 10 Tips to Create the TExES Core Subjects Math Study Plan
























What people say about "How to Add Polynomials to Find Perimeter - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.