How to Solve Parallel Lines and Transversals Problems? (+FREE Worksheet!)

When a line (transversal) intersects two parallel lines in the same plane, eight angles are formed. In this article, we will teach you how to find the missing angles in this case by using the Parallel Lines and Transversals rules.
Related Topics
- Special Right Triangles
- How to Solve Triangles Problems
- How to Find Volume and Surface Area of Cubes
- How to Calculate Cylinder Volume and Surface Area
- How to Find Complementary and Supplementary Angles
A step-by-step guide to solving Parallel Lines and Transversals Problem
- When a line (transversal) intersects two parallel lines in the same plane, eight angles are formed. In the following diagram, a transversal intersects two parallel lines. Angles 1, 3, 5, and 7 are congruent. Angles 2, 4, 6, and 8 are also congruent.
- In the following diagram, the following angles are supplementary angles (their sum is 180):
• Angles 1 and 8
• Angles 2 and 7
• Angles 3 and 6
• Angles 4 and 5
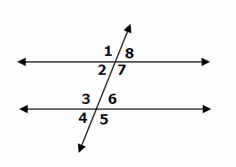
Examples
Parallel Lines and Transversals – Example 1:
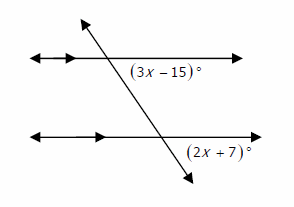
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?
Solution:
The two angles \(3x-15\) and \(2x+7\) are equivalent.
That is: \(3x-15=2x+7\)
Now, solve for \(x: 3x-15+15=2x+7+15 →\)
\(3x=2x+22→3x-2x=2x+22-2x→x=22\)
Parallel Lines and Transversals – Example 2:
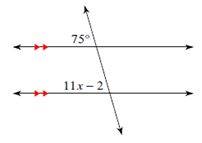
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?
Solution:
The two angles \(75^\circ\) and \(11x-2\) are equal. \(11x-2=75\)
Now, solve for \(x: 11x-2+2=75+2→ 11x=77→x=\frac{77}{11}→x=7\)
Parallel Lines and Transversals – Example 3:
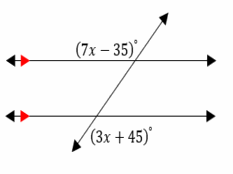
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?
Solution:
The two angles \(7x-35\) and \(3x+45\) are equivalents.
That is: \(7x-35=3x+45\)
Now, solve for \(x: 7x-35+35=3x+45+35 →\)
\(7x=3x+80→7x-3x=3x+80-3x→4x=80→x=\frac{80}{4}→x=20\)
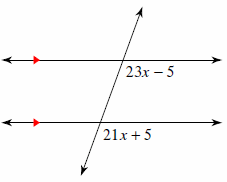
Parallel Lines and Transversals – Example 4:
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?
Solution:
The two angles \(3x-27\) and \(-x+33\) are equivalents.
That is: \(3x-27=-x+33\)
Now, solve for \(x: 3x-27+27=-x+33+27 →\)
\(3x=-x+60→3x+x=-x+60+x→4x=60→x=\frac{60}{4}→x=15\)
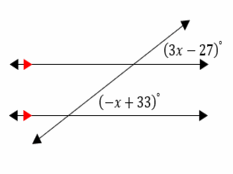
Exercises for Parallel Lines and Transversals
Find missing angles with Parallel Lines and Transversals.
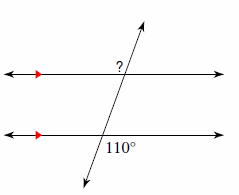
1.Find the measure of the angle indicated.
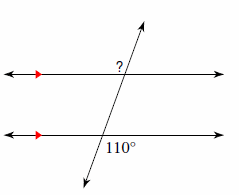
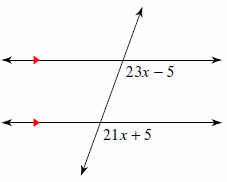
2. Solve for \(x\).
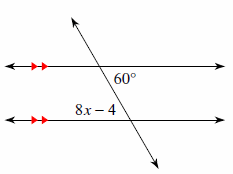
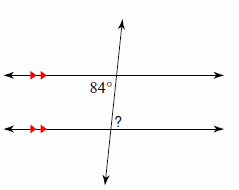
3. Find the measure of the angle indicated.
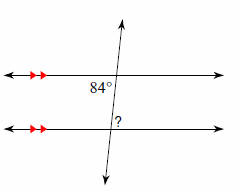
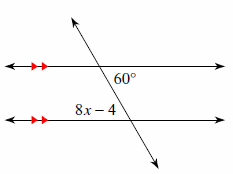
4. Solve for \(x\).

1.\(\color{blue}{110^\circ}\)
2.\(\color{blue}{x=8}\)
3. \(\color{blue}{84^\circ}\)
4.\(\color{blue}{x=5}\)
Related to This Article
More math articles
- CLEP College Math Practice Test Questions
- The Ultimate 7th Grade MCAP Math Course (+FREE Worksheets)
- Comparison and Number Ordering
- The Ultimate CLEP College Algebra Formula Cheat Sheet
- The Ultimate PSAT Math Course (+FREE Worksheets & Tests)
- 6th Grade ISTEP Math Worksheets: FREE & Printable
- HiSET Math – Test Day Tips
- How to Master the World of Conjectures and Counterexamples
- Integrals: Everything You Need To Know
- How to Study Math Like a Pro









What people say about "How to Solve Parallel Lines and Transversals Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.